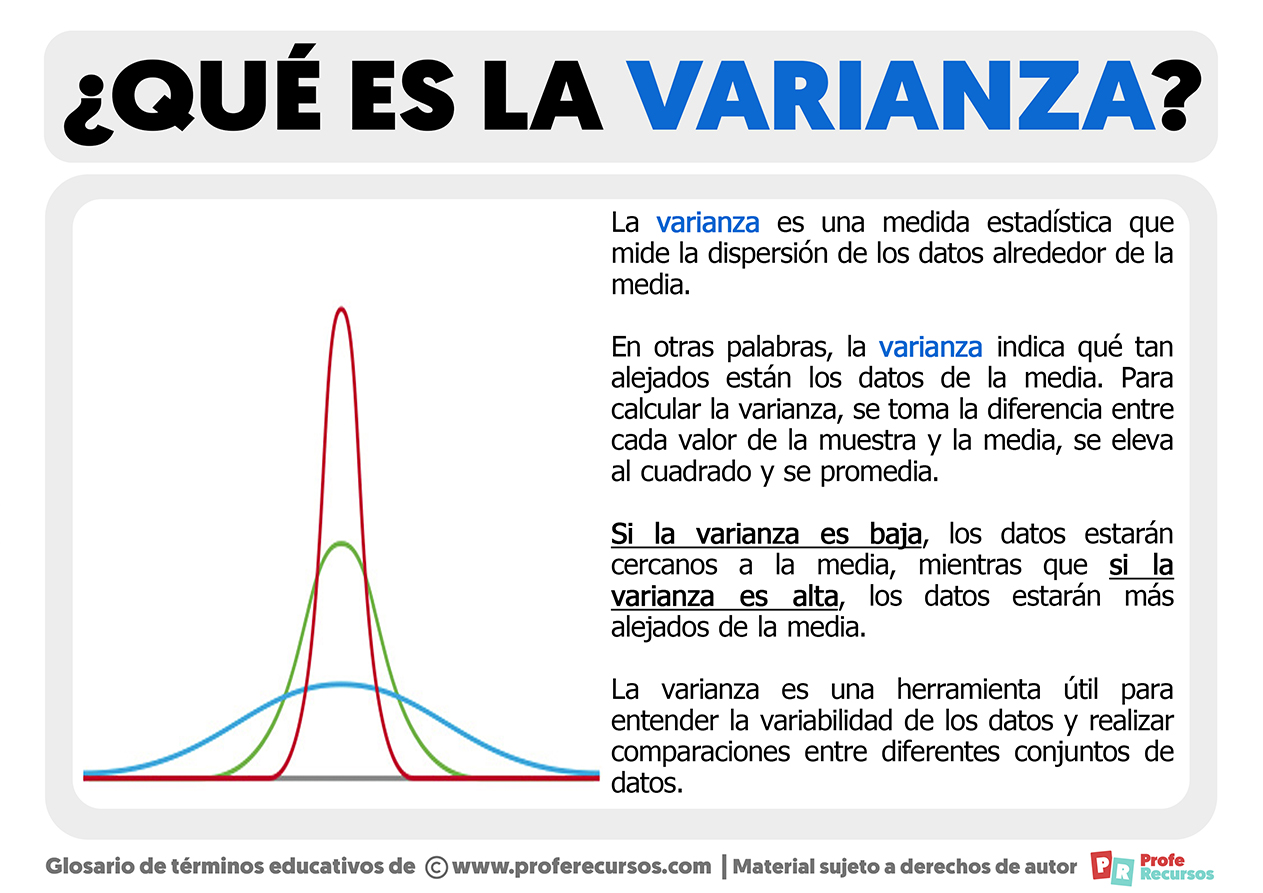
La varianza es una medida estadística que mide la dispersión de los datos alrededor de la media. Es decir, la varianza indica qué tan alejados están los datos de la media.
¿Cómo calculamos la Varianza de una muestra?
Para calcular la Varianza, se toma la diferencia entre cada valor de la muestra y la media, se eleva al cuadrado y se promedia.
- Si la Varianza es baja, los datos estarán cercanos a la media.
- Mientras que si la Varianza es alta, los datos estarán más alejados de la media.
La fórmula matemática de la Varianza es la siguiente:
Varianza = Σ(xi – x)^2 / n
Ejemplo para calcular la Varianza
Supongamos que tienes las siguientes notas de 10 alumnos en un examen de matemáticas:
7, 8, 5, 9, 6, 6, 8, 7, 8, 9
Primero calculamos la media de estas notas, que es 6.7. A continuación, calculamos las desviaciones de cada dato respecto a la media, elevando al cuadrado la diferencia entre cada dato y la media:
- (7-6.7)^2 = 0.09
- (8-6.7)^2 = 1.69
- (5-6.7)^2 = 2.89
- (9-6.7)^2 = 5.29
- (6-6.7)^2 = 0.49
- (6-6.7)^2 = 0.49
- (8-6.7)^2 = 1.69
- (7-6.7)^2 = 0.09
- (8-6.7)^2 = 1.69
- (9-6.7)^2 = 5.29
Luego, sumamos todas las desviaciones al cuadrado:
0.09 + 1.69 + 2.89 + 5.29 + 0.49 + 0.49 + 1.69 + 0.09 + 1.69 + 5.29 = 19.01
Finalmente, dividimos la suma de las desviaciones al cuadrado entre el número total de datos (10) para obtener la Varianza:
Varianza = 19.01 / 10 = 1.901
Por lo tanto, la Varianza de las notas de los 10 alumnos en este examen de matemáticas es 1.901.




Deja tu comentario