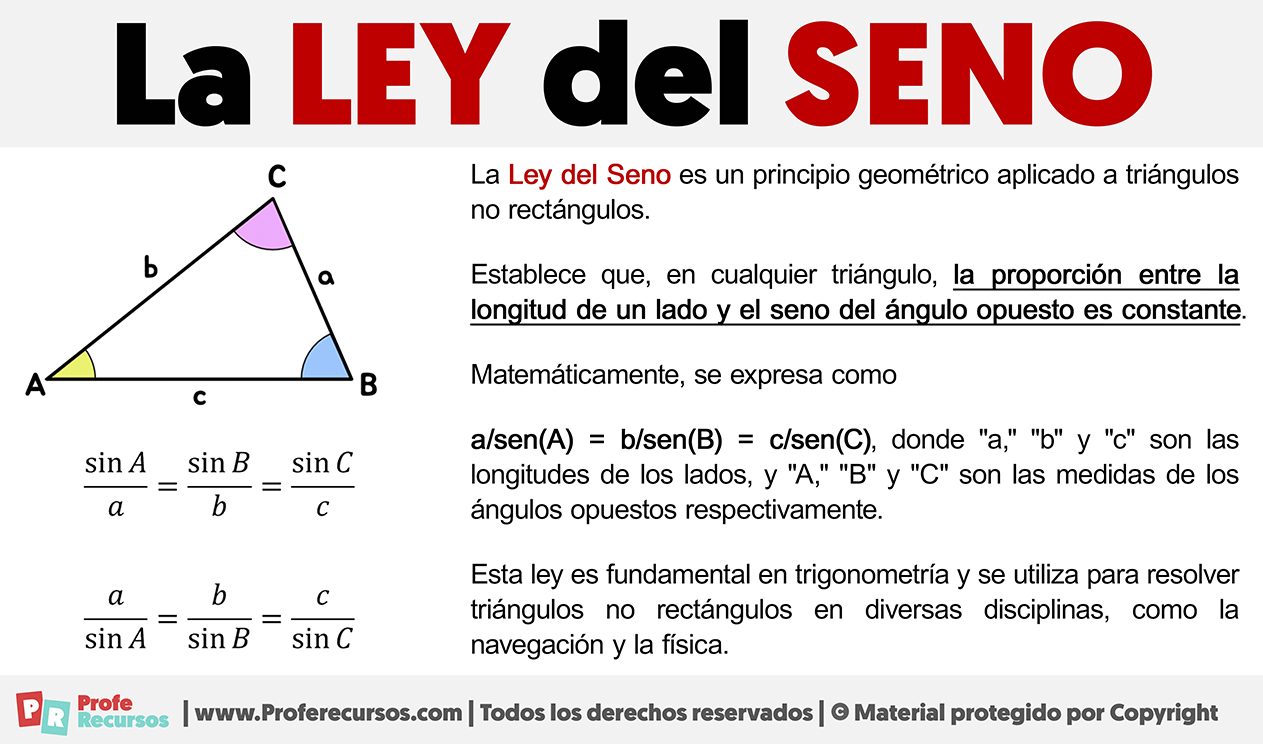
La Ley del Seno es un principio geométrico aplicado a triángulos no rectángulos. Esta ley establece que, en cualquier triángulo, la proporción entre la longitud de un lado y el seno del ángulo opuesto es constante.
Matemáticamente, se expresa como
a/sen(A) = b/sen(B) = c/sen(C)
donde «a,» «b» y «c» son las longitudes de los lados, y «A,» «B» y «C» son las medidas de los ángulos opuestos respectivamente.
Esta ley es fundamental en trigonometría y se utiliza para resolver triángulos no rectángulos en diversas disciplinas, como la navegación y la física.
Veamos un ejemplo del teorema del seno
Supongamos que en el triángulo ABC, el ángulo A es de 30 grados, el lado opuesto a este ángulo (a) mide 4 unidades, y el ángulo B es de 50 grados, con el lado opuesto a este ángulo (b) de 6 unidades.
Queremos encontrar la longitud del lado c opuesto al ángulo C.
Usamos la Ley de Senos: a/sen(A) = b/sen(B) = c/sen(C).
Sustituimos valores: 4/sen(30) = 6/sen(50) = c/sen(C).
Resolvemos para c:
c = sen(C) * (4/sen(30)) = sen(C) * (6/sen(50)).
Esto nos ayuda a hallar la longitud del lado c opuesto al ángulo C.



Deja tu comentario