El máximo común divisor (MCD) es el mayor número entero que divide exactamente a dos o más números. En otras palabras, es el número más grande que es un divisor común de esos números.
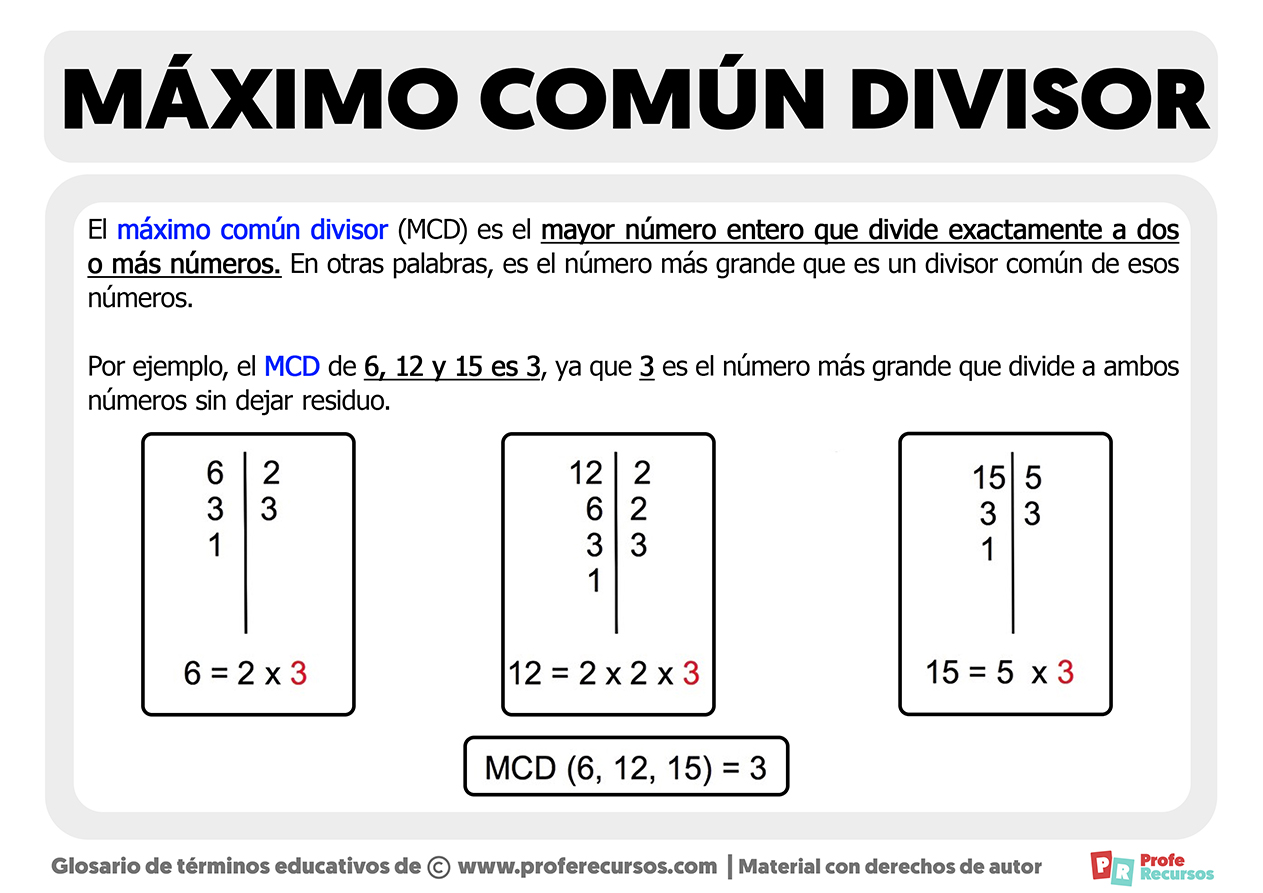
Por ejemplo, el MCD de 6, 12 y 15 es 3, ya que 3 es el número más grande que divide a ambos números sin dejar residuo.
Vamos a verlo explicado paso a paso para comprender el proceso.
Ejemplo: Calcular el MCD de 6,12 y 15
Para calcular el máximo común divisor (MCD) de tres números, en este caso, 6, 12 y 15, podemos seguir el proceso de descomposición en factores primos y luego identificar los factores comunes con las menores potencias.
Paso 1: Descomponemos cada número en sus factores primos:
- 6 = 2 * 3
- 12 = 2 * 2 * 3
- 15 = 3 * 5
Paso 2: Identificamos los factores comunes.
Ahora, identificamos los factores primos que se repiten en los tres números y tomamos las menores potencias:
- Los factores primos comunes son: 2 y 3.
- La menor potencia del factor 2 es 2^1 (porque aparece una vez en 6 y dos veces en 12, pero tomamos la menor).
- La menor potencia del factor 3 es 3^1 (aparece una vez en cada número).
Paso 3: Calcular el MCD
Finalmente, calculamos el máximo común divisor (MCD) multiplicando los factores primos comunes con sus menores potencias:
MCD(6, 12, 15) = 2^1 * 3^1 = 2 * 3 = 6
Por lo tanto, el máximo común divisor de 6, 12 y 15 es 6.



Deja tu comentario